Artificial Intelligence, Machine learning, Technology

Learn Everything About Feature Scaling

Posted on by Febronei
29
Mar

Feature Scaling?

Feature scaling is a technique used when we create a machine learning model. It lets you to normalize the range of independent variables or features of the given field of the dataset. It is also known as data normalization. During data preprocessing phase, it is important to do data normalization because, machine learning algorithm will not perform well if the data attributes have different scales.

let’s scratch the surface…

Why Feature Scaling is Important?

The importance of feature scaling is can be illustrated by the following simple example.

Suppose in a dataset we have features and  each feature has different records.

featuresf1f2f3f4f5
Magnitude3004001520550
UnitKgKgcmcmg

Remember every feature has two components

  • Magnitude  (Example: 300)
  • Unit (Example: Kg)

Always keep in mind: Most of the ML algorithms work based on Euclidean distance, Manhattan distance or K Nearest-Neighbors and few others.

featuresf1f2f3f4f5 (f2- f1) (f4- f3)
Magnitude3004001520550400-300 = 10020-15=5
UnitKgKgcmcmgKgcm

So coming back to this example, so when we try to find out the distance between different features, the gap between them actually varies. Some attributes have large gap in between while others are very close to each other. See the table:

You may also have noticed, unit of f5 is in gram(g) while f1 and f2 are in Kilo gram (Kg). So in this case, the model may consider the value of f5 is greater than f1 and f2 but that’s not the case. Because of these reasons, the model may give a wrong predictions.

Therefore we need to make all the attributes (f1, f2, f3…) to have same scale with respect to its units.  In short, we need to convert all the data into same range (usually between 0-1)  such that no particular feature gets dominant over another or no particular feature has less dominant. (By doing so, the convergence will be also much fast and efficient).

There are two common methods used to get all attribute into same scale.

Min-max Scaling

In min-max scaling, values are rescaled to a range between 0 to 1. To find the new value,  we need to subtracting the min value and then divide by the max minus the min. Scikit-Learn provides MinMaxScaler for this calculation.


    \[X_{new} = \frac{ Xi-min(X)}{max(X)-min(X)}\]

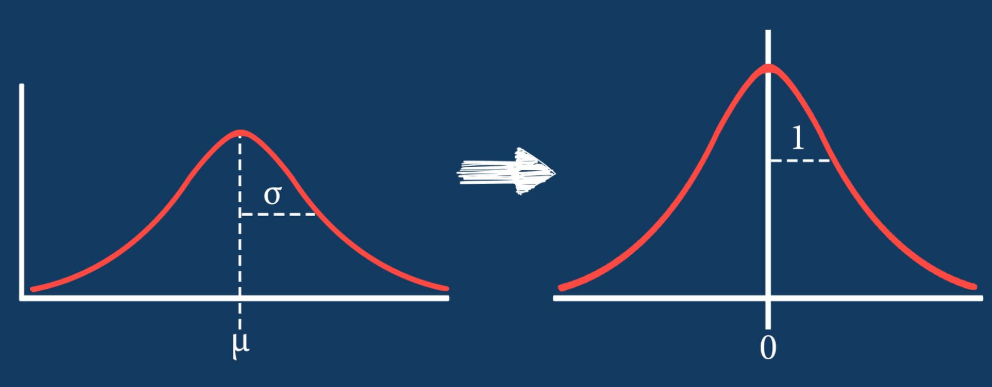
Standardization

Standardization is much less affective by outliers (explain outliers – link) . First we need subtract the mean value then divide by standard deviation such that it forms resulting distribution of unit variance. Scikit-Learn provides  a transformer called StandardScaler for this calculation.


    \[ X_{new} = \frac{Xi-X_{mean}}{Standard Deviation} \]

Here I show an example for feature scaling using min-max scaling and standardization. I’m using google colab but you can use any notebook/Ide such as Jupyter notebook or PyCharm.

Go to the link and download Data_for_Feature_Scaling.csv

Upload csv to the google drive

Mount drive to the working notebook

For that you may need authorization code from google Run the code.

# feature scaling sample code
# import recommended libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import preprocessing
# mount drive
from google.colab import drive
drive.mount('/content/drive')
# import dataset 
data_set = pd.read_csv('feature_scaling/Data_for_Feature_Scaling.csv')
# check the data 
data_set.head()
Output
        Country	 Age	Salary	Purchased
0	France	 44	72000	0
1	Spain	 27	48000	1
2	Germany	 30	23000	0
3	Spain	 38	51000	0
4	Germany	 40	1000	1
x = data_set.iloc[:, 1:3].values
print('Origianl data values: \n', x)
Output
Original data values: 
 [[  44   72000]
 [   27   48000]
 [   30   23000]
 [   38   51000]
 [   40    1000]
 [   35   49000]
 [   78   23000]
 [   48   89400]
 [   50   78000]
 [   37   9000]]
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler(feature_range=(0, 1))
# Scaled feature 
x_after_min_max_scaler = min_max_scaler.fit_transform(x)
print('\n After min max scaling\n', x_after_min_max_scaler)
Output
After min max scaling
 [[0.33333333  0.80316742]
 [0.           0.53167421]
 [0.05882353   0.24886878]
 [0.21568627   0.56561086]
 [0.25490196   0.        ]
 [0.15686275   0.54298643]
 [1.           0.24886878]
 [0.41176471   1.        ]
 [0.45098039   0.87104072]
 [0.19607843   0.09049774]]
# Now use Standardisation method
Standardisation = preprocessing.StandardScaler()
x_after_Standardisation = Standardisation.fit_transform(x)
print('\n After Standardisation: \n', x_after_Standardisation)
Output
After Standardisation: 
 [[ 0.09536935  0.97512896]
 [-1.15176827   0.12903008]
 [-0.93168516  -0.75232292]
 [-0.34479687   0.23479244]
 [-0.1980748   -1.52791356]
 [-0.56487998   0.1642842 ]
 [ 2.58964459  -0.75232292]
 [ 0.38881349   1.58855065]
 [ 0.53553557   1.18665368]
 [-0.41815791  -1.2458806 ]]

Learning resources: